
the First Six Books, Together with the Eleventh and Twelfth. In geometry, it is possible to bisect many objects using just a compass and ruler.

Robert Simson, (181) The Elements of Euclid, viz. Diameter PQ bisects circle O : Segment RT bisects triangle PQR: Constructing bisectors.
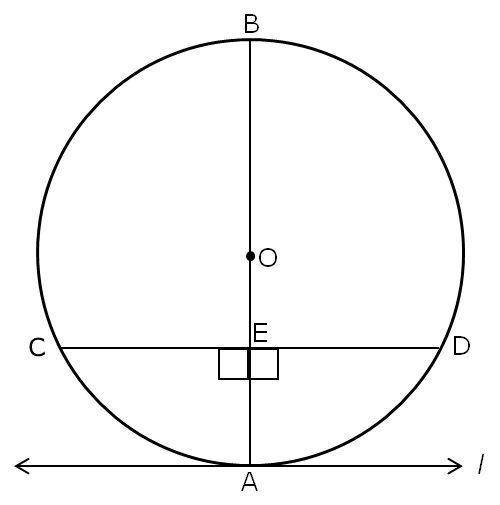
Similar segments of circles on equal straight lines equal one another. If AB is a chord of a circle with center O (but not a diameter), the ray OM, through the midpoint M of AB bisects the angle AOB. Therefore, the two semicircles of a circle are similar segments. Similar segments of circles are those which admit equal angles, or in which the angles equal one another. In a circle the angle in the semicircle is right, that in a greater segment less than a right angle, and that in a less segment greater than a right angle further the angle of the greater segment is greater than a right angle, and the angle of the less segment is less than a right angle. We do not know that the semicircle is "half" of a circle. And the center of the semicircle is the same as that of the circle. Then again, Euclid skipped over other things like needing to assume that the plane was complete. A semicircle is the figure contained by the diameter and the circumference cut off by it. One of the major contributions Thales is said to have given is the proof that a diameter of a circle bisects the circle, yet Euclid doesn't even bat an eye.


 0 kommentar(er)
0 kommentar(er)
